por João Cortese
Sempre se comentou os filmes que chegam às telas dos cinemas; hoje, acrescentou-se a esta uma outra categoria: os filmes que chegam aos serviços de vídeo por internet. Pois bem: trata-se de O homem que viu o infinito (The man who knew infinity, com o famigerado pesar de tradução nacional de títulos), película de 2015. Cabe ressaltar que, cinematograficamente, o filme não tem nada de espetacular. Mas a história verídica na qual se baseia tem!

“Permita que me apresente: sou escriturário do Departamento de Contas do Escritório portuário de Madras, com um salário de apenas £20 por ano”: assim se apresentou Srinivasa Ramanujan em uma carta ao grande matemático G. H. Hardy, de Cambridge. Seria difícil suspeitar de que aquele indiano viveria apenas 32 anos, descobrindo porém quase quatro mil resultados matemáticos.
Ramanujan foi um matemático para quem os números possuíam individualidades próprias, e com os quais o homem podia se relacionar. Um mundo no qual poderia parecer difícil de entrar: “eu quero entender mais do que apenas cores que não posso ver”, reclama a Ramanujan sua esposa, numa cena do filme. Mostrando-lhe a areia da praia, este lhe diz: “imagine se pudéssemos olhar tão de perto a ponto de ver cada grão, cada partícula. Você veria que há padrões em tudo”. A matemática, mostrou Ramanujan, seria um modo de revelar estes padrões de uma maneira bela.

Algumas das descobertas feitas por Ramanujan são compreensíveis aos mortais com uma formação básica em matemática. Em uma circunferência qualquer, se dividimos sua circunferência por seu diâmetro, encontramos o número que foi denominado ?. Expressar tal número é um problema, pois, sendo irracional, ele tem infinitas casas depois da vírgula, e que não seguem ordem lógica alguma. Algumas das fórmulas de Ramanujan permitem exprimir tal número com somas infinitas.
Após a famosa carta, que era acompanhada de algumas descobertas notáveis, Ramanujan foi convidado por Hardy a trabalhar com ele em Cambridge. No Trinity College, ele entrou em contato não apenas com Hardy, mas também com o matemático John Littlewood e com o filósofo Bertrand Russell. O college tinha tradição: haviam estado lá, por exemplo, ninguém menos que Newton e Maxwell.

A viagem entre a colônia e a metrópole foi de seis mil milhas – algo com que Ramanujan diz no filme não se preocupar, pois conhecia números maiores. Mas a maior distância no caso é a cultural. O indiano e o inglês encontram-se em Cambridge: o primeiro se satisfaz em chegar aos resultados matemáticos pela intuição, sem requerer justificativas posteriores; o segundo crê que isto é incompleto se não houver uma demonstração rigorosa de que tais resultados são verdadeiros. “Eu suponho que é sempre difícil para um inglês e um indiano entenderem-se adequadamente”, diz o personagem de Hardy no filme. Mas a matemática poderia ser distinta para cada nacionalidade? “Verdade aquém dos Pireneus, erro além”, Pascal escrevia em seus Pensamentos. A verdade seria assim dividida por uma montanha?
Quando Hardy pergunta a Ramanujan como ele chegou a um certo teorema matemático, ele responde: “eu apenas sei”. Mas a intuição não é uma justificativa suficiente para Hardy, que como a maior parte dos matemáticos vê a necessidade de demonstrações para qualquer resultado matemático válido. “O objetivo do rigor matemático é o de sancionar e de legitimar a conquista da intuição, e ele não teve nunca outra finalidade”, escrevia J. Hadamard no seu Ensaio sobre a psicologia da invenção no domínio matemático.
A questão pode ser melhor contemplada se lembrarmos algumas das indagações filosóficas colocadas à matemática: sobre o que ela fala? Há uma verdade independente dos conteúdos matemáticos, aos quais o homem deve fazer justiça em seu conhecimento, ou a matemática não é mais do que uma construção formal humana, e portanto uma convenção?
Caso haja uma verdade independente da construção matemática – o que nos permitiria falar em “descoberta”, ao invés de “invenção” –, como entretanto acessar esta verdade? Uma versão comumente aceita da história da matemática é que esta tem um ponto de virada com os gregos, que introduziram a noção de demonstração: um procedimento seguro que nos permite saber por que acreditar em um certo conteúdo e em quais outras noções ele se baseia. Mas diz-se também que os gregos aprenderam muito da geometria egípcia, a qual não teria por sua vez demonstrações. Ainda assim, os terrenos eram calculados após cada cheia do Nilo sem erros, e os egípcios teriam conhecido mesmo o teorema que ligamos ao nome de Pitágoras. Isto já não teria uma importância em si?
Qual é então o valor de uma verdade matemática sem demonstração? O engenheiro, o economista, quiçá mesmo o físico, sem perda de dignidade do ofício, não necessitam conhecer a fundamentação do cálculo integral e diferencial pela disciplina matemática da análise para poder construir pontes, gerir bolsas ou encontrar uma partícula. Basta que estejam seguros de que esta teoria é válida.
Mas isto não faz apenas transferir o problema? Alguém (no caso, um matemático), teve de verificar este resultado. O que ocorre neste caso é unicamente uma transferência da verificação entre campos do saber, cada parte do edifício dependendo de uma disciplina. Mas a matemática continua, nesta imagem, nas fundações do prédio. De fato, o sistema axiomático-dedutivo dos Elementos de Euclides, que demonstra todas as proposições a partir de axiomas, serviu de base a boa parte das ciências ocidentais. A tarefa do matemático puro, para muitos, está associada a assegurar resultados a partir de afirmações primeiras que são consideradas válidas – ou seja, por demonstrações. Ao considerarmos uma fórmula para infinitos casos, uma demonstração garante que ela será sempre válida, e não apenas até o número 517.348 (e, acredite, neste domínio surpresas acontecem).
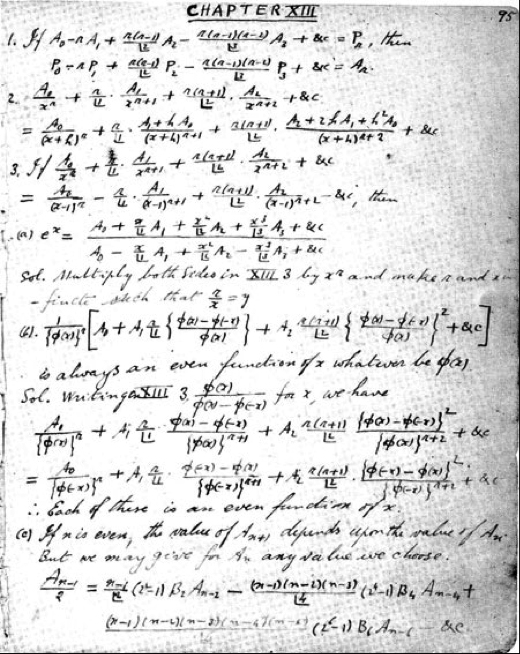
Ganhamos assim a justificativa; mas seria ela a única via para a verdade? Não para Ramanujan, que vai contra a imagem padrão da matemática como demonstrativa: “Sr. Hardy, Não entendo por que perdemos nosso tempo calculando todas essas provas. Eu tenho as fórmulas”, diz ele a Hardy no filme, ao que este responde: “não é que eu discorde do que você afirma. É que não tenho certeza de como você chegou lá, ou se suas afirmações estão corretas”. Em um momento, Hardy revela a Ramanujan que um de seus teoremas sobre os números primos está errado, o que foi demonstrado por Littlewood. Evidencia-se assim que a questão da balança entre a intuição da verdade e a demonstração desta não é assim tão simples: a intuição de fato não dá segurança absoluta à matemática pura, cujos resultados são frequentemente inesperados; por outro lado, se Ramanujan tivesse de demonstrar todos os seus resultados, provavelmente não os teria encontrado em tão grande número.
Questionado certa vez sobre a origem de uma das equações que ele descobrira, Ramanujan respondeu que sua deusa Namagiri tinha lhe aparecido num sonho e lhe ajudado a resolver o problema. A intuição, se é que se poderia falar neste termo aqui, parece ir infinitamente além do que uma receita de bolo para encontrar resultados matemáticos.
Por outro lado, cabe lembrar que, se o matemático ocidental típico demanda demonstrações para justificar a verdade de seus teoremas, nenhuma teoria parece dar totalmente conta de como ele chegou a esses resultados. Um grande avanço foi feito nos últimos anos rumo a demonstradores computacionais de teoremas matemáticos – mas as demonstrações de diversos teoremas resistem a eles. A questão é portanto mais intrincada do que aparenta – o suficiente para autores como Karl Popper negarem o estudo da descoberta científica ao âmbito da filosofia, crendo ser impossível um tratamento racional de tal processo. Só estaria acessível à filosofia da ciência o contexto da justificativa, e não aquele da descoberta.
Ramanujan fez grandes contribuições para áreas de matemática, como a teoria analítica dos números, as funções elípticas, frações contínuas e séries infinitas. Uma de suas contribuições foi sobre as partições. Uma partição de um número n é um conjunto de números cuja soma é igual a este número n. As partições de 4, por exemplo, são 3+1, 2+2, 2+1+1, 1+1+1+1 e o próprio número 4. Se designamos uma função partição por p(n), a qual indica o número de partições de um número n, então p(4) = 5, pois temos cinco combinações de somas que resultam no número 4. Tal função cresce de maneira rápida: quando calculamos as partições do número 100, por exemplo, encontramos p (100) = 204.226 combinações. Mas os matemáticos não conheciam nenhuma fórmula para tal função, e calculavam independentemente a partição de cada número. Até que em 1918 Ramanujan encontrou uma fórmula válida para qualquer um dos infinitos números naturais:
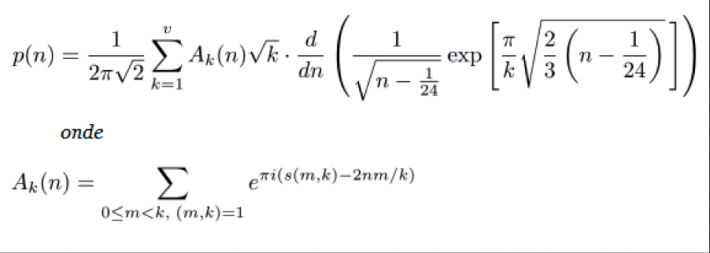
No filme, quando Hardy lhe pergunta por que faz o que faz, Ramanujan responde: “porque tenho de fazê-lo. Eu o vejo”. Hardy atribui então a Ramanujan um amor pela forma, como o tiveram matemáticos como Euler e Jacobi. “A forma pela forma, uma arte por si própria”, diz Hardy a respeito da atividade de Ramanujan, completando: “e, como toda arte, ela revela a verdade”. Hardy, no filme, declara ainda: “é a minha única verdade, minha igreja”. A matemática pura apareceria, assim, como uma busca por uma verdade exclusiva a ela. Quanto a Ramanujan, atribui-se a ele a frase: “uma equação não significa nada para mim, a não ser que ela expresse um pensamento de Deus”.
“Eu bem vejo que a verdade é a mesma em Toulouse e em Paris”, escrevia Pascal a Fermat, matemático sediado no sul da França, ao saber que haviam concordado sobre um novo resultado matemático. Pode-se, afinal, questionar se de fato uma alta montanha demoveria a verdade.
Cabe ainda lembrar a frase de Russell citada no início do filme: “a matemática, vista corretamente, possui não apenas verdade, mas também suprema beleza”. Ramanujan foi um dos matemáticos que conseguiram revelar tal beleza ao mundo.
Para saber mais:
• Doxiads, A. K., Papadimitriou, C. H., Papadatos, A., Di Donna, A., & Santos, A. B. Logicomix: uma jornada épica em busca da verdade. WMF Martins Fontes, 2000. (Trata-se de uma história em quadrinhos primorosa, apresentando a vida de Bertrand Russell conjuntamente à história da lógica no século 2o)
• Pi, filme de Darren Aronofsky de 1998.
• Kanigel, R. The man who knew infinity: a life of the genius Ramanujan. New York : Charles Scribner’s Sons, 1991.
• Hardy, G. H. Em defesa de um matemático. Martins Fontes, 2000.
• Silva, J. J. da. Filosofias da matemática. São Paulo: UNESP, 2007.