por Felipe Pait
A inteligência artificial engloba um conjunto de tecnologias entrelaçadas, com nomes como aprendizado mecânico, ciência dos dados, engenharia da informação, redes neurais artificiais, “big data”, “deep learning”, e “data mining”, entre outros, que passam por um desenvolvimento acelerado com aplicações que vão influenciar todas as áreas de atividade. Frequentemente vemos previsões de que a inteligência artificial num certo momento superará a humana. Ou, ao contrário, que uma determinada atividade requer um tipo de inteligência que somente o ser humano possui, sendo imune ao avanço da tecnologia. Para nos contrapormos a tais especulações, é necessário pensar sobre a forma como as tecnologias são construídas e aplicadas. Nesse artigo, vamos dar alguns exemplos intuitivos de uso de aprendizado mecânico, retomar algumas lições da estatística tradicional e, ao final, sugerir que a combinação entre elas permite lidar com problemas matemáticos realmente complexos.
Os especialistas em computação projetam programas de computador que recebem entradas e produzem saídas. As entradas são os dados fornecidos pelo usuário, e as saídas são as respostas desejadas. No caminho entre receber as entradas e prover as saídas, o programa executa operações e cálculos especificados por quem desenvolveu a tecnologia. A melhor forma de descrever o programa, então, é considerar quais os dados de entrada a serem fornecidos, e qual a pergunta que desejamos responder usando o computador. Consideremos agora algumas aplicações comuns do atual estágio da tecnologia de inteligência artificial. Vamos descrever, de forma esquemática, a partir de seis exemplos, as informações que temos disponíveis e explicitar a pergunta que queremos responder a partir delas.
Dado: uma amostra de tecido celular obtida em exame médico por meio de biópsia.
Pergunta: o tecido contém células alteradas ou tumorais?
A partir da classificação automática, o médico pode direcionar seus esforços para o diagnóstico dos casos que inspiram mais cuidados.
Dado: uma imagem telescópica.
Pergunta: a imagem representa fenômenos astronômicos raros ou de curta duração, como explosões estelares denominadas supernovas?
É impossível para os astrônomos monitorar todas as imagens feitas por telescópios. A identificação automática de fenômenos especiais permite redirecionar as observações sem desperdiçar oportunidades únicas.
Dado: histórico de operações de entrada e saída executadas pelo sistema operacional de um computador, respondendo a chamadas dos aplicativos.
Pergunta: algum dos processos em execução é invasivo, ou contém um código malicioso, como vírus ou malware?
A classificação dos programas serve de alerta para limpeza ou manutenção apropriada do hardware e do software do computador.
Dado: a disposição de pedras em um tabuleiro do jogo de Go, discutido no artigo “O Mestre de Go”, aqui no Estado da Arte em julho de 2017.
Pergunta: a configuração é mais favorável às pedras brancas ou às negras para conseguir seus objetivos de conquistar um território superior?
Obter uma resposta para essa dificílima pergunta torna um programa que joga Go quase imbatível.
Dado: uma fotografia de um documento histórico manuscrito.
Pergunta: qual a sequência de letras do texto?
A reprodução do conteúdo do texto, mesmo que cheia de erros, facilita a busca pelos documentos primários relevantes para um estudo histórico específico.
Dado: a atividade de um grupo de indivíduos nas redes sociais, obtida por meio lícitos ou sub-reptícios.
Pergunta: quais são suscetíveis a campanhas de desinformação, constrangimento, e intimidação por meio de notícias falsas?
A identificação dos indivíduos suscetíveis pode ser usada para influenciar escolhas eleitorais.
Em cada um desses exemplos está disponível uma grande quantidade de informações, cuja análise exigiria muito trabalho. Um programa de computador capaz de processar e classificar o conjunto de dados pode servir para uma análise preliminar, permitindo que o especialista concentre seus esforços nos casos mais importantes. Ou então servir de entrada para outro programa que executa ações específicas dependendo do resultado da análise automática. É indiscutível que aprender a executar cada uma dessas tarefas exige inteligência do ser humano, o que também é verdade a respeito de todos os cálculos, para nós complexos, que hoje são executados rapidamente por computadores. A construção de um programa de inteligência artificial consiste em especificar os cálculos que produzem as respostas desejadas a partir dos dados fornecidos.
Os exemplos se referem a problemas de classificação, como tipicamente faz a inteligência artificial mais moderna. Em alguns exemplos a classificação é binária, com uma resposta “sim ou não”, possivelmente acompanhada de uma indicação de confiança. Em outros pode haver classificação entre diversos grupos ou tipos de dados de entrada. Conforme apresentado no artigo “Regressão, classificação, e aprendizado por máquina”, publicado aqui no Estado da Arte em junho de 2018, a estatística clássica tende a usar mais os procedimentos de modelagem, conhecidos como regressão linear, embora a classificação utilize ferramentas matemáticas semelhantes. Isso ocorre porque nos modelos lineares as inclinações e tendências a subida e descida têm interpretações diretas. Nos problemas mais complexos da ciência dos dados, uma simples classificação já constitui um apoio considerável para tomada de decisões.
Uma ilustração da diferença entre classificação e regressão aparece em dois gráficos produzidos pelo cientista político Jairo Nicolau, autor de diversos livros e artigos sobre eleições e sobre visualização de dados, e do prefácio da tradução brasileira “Como as democracias morrem” do livro de S. Levitsky e D. Ziblatt discutido aqui em fevereiro de 2018. O primeiro gráfico, divulgado via Twitter, mostra uma relação linear crescente entre o tempo de televisão e a fração de votos obtida por candidatos a presidência do Brasil em eleições desde 1989. Num tweet imediatamente posterior, o cientista político faz uma versão simplificada e de mais fácil interpretação, onde os candidatos são classificados em 2 grupos, os que ficaram em primeiro ou segundo lugar no primeiro turno das eleições, e os demais, revelando mais claramente a correlação entre as variáveis. A classificação, que facilita a interpretação dos dados, no caso foi feita usando informação extra, e não de modo automático. Vale a pena sempre notar que correlação não implica causalidade. Os candidatos recebem mais votos porque aparecem mais na televisão? Ou têm mais tempo de propaganda por terem conseguido montar coalizões mais amplas, com maior potencial de atrair eleitores? Ou será que o efeito de outros fatores é mais importante?
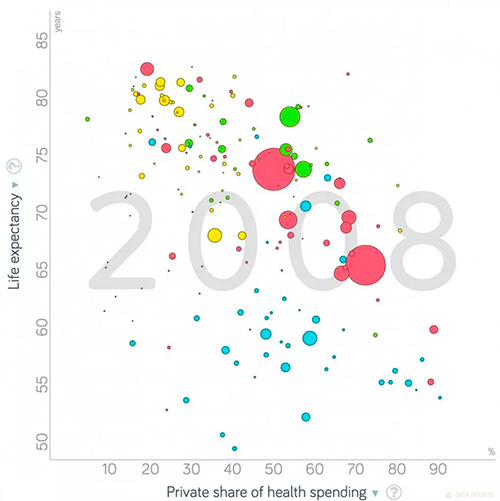
Vamos continuar a ilustrar alguns desafios para a obtenção de modelos com três gráficos simples mas reveladores, que podem ser obtidos gratuitamente da página da organização independente sueca Gapminder. Mostramos aqui dados de 2008, que são mais completos, sendo que a página www.Gapminder.org apresenta mais informação. O primeiro mostra a relação entre a expectativa de vida e a fração dos gastos em saúde que provém de fontes privadas, em dezenas de países. Os círculos representando países têm tamanho proporcional à população de cada país e são coloridos de acordo com os continentes. É claramente visível que a expectativa de vida é maior em países onde o gasto em saúde é predominantemente público. Porém a obtenção de um valor numérico para a inclinação da reta de regressão, ou do coeficiente de correlação, fica pouco precisa se deixarmos de fazer um passo intermediário, a classificação. É visível que os países formam 2 grupos. Em alguns deles, a maioria na África subsaariana, a expectativa de vida é baixa, possivelmente por fatores ambientais e econômicos (os países da África estão indicados em azul). Nos demais fica claríssimo que uma alta fração de gastos privados em saúde corresponde a menor longevidade. Uma investigação da origem desse fenômeno exigiria uma análise multivariada, multidimensional, usando ferramentas matemáticas mais complexas do que um gráfico no plano. O desafio para a engenharia do aprendizado mecânico é desenvolver técnicas que combinem regressão e classificação, podendo fazer uso de modelos não lineares, e identificando padrões automaticamente, sem a necessidade da intervenção humana.
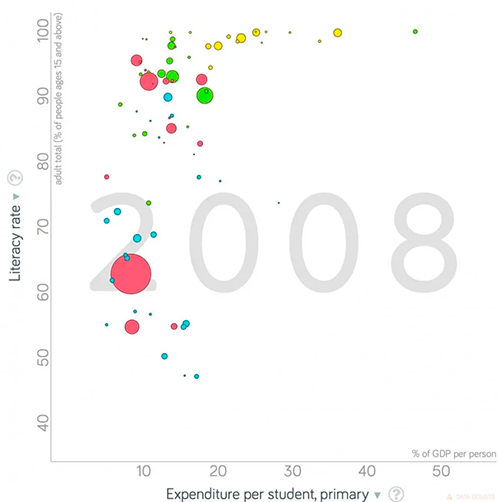
Outro gráfico interessante mostra que quanto maior o gasto por estudante no ensino fundamental, expresso como fração da renda per capita, maior a taxa de alfabetização em um país. O fato não é surpreendente, porém devemos notar que nenhum modelo linear descreve os dados fidedignamente – nem poderia, já que a alfabetização não passa de 100%, mas os gastos em educação podem variar muito. Qual é então o tipo de modelo matemático, certamente não-linear, mais apropriado para estudar automaticamente a relação entre esses dados?
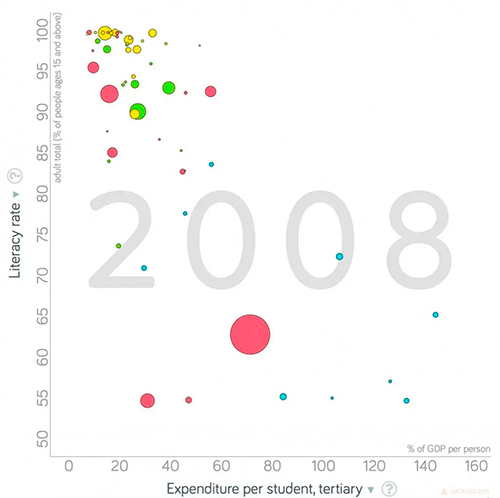
Já os gastos com educação superior mostram um efeito distinto, e talvez surpreendente. De fato, quanto maiores os gastos por estudante do ensino superior, medidos como fração da renda per capita, maior o analfabetismo! Repetimos sempre que a relação entre causa e efeito não é imediata, uma vez que as variáveis apresentadas não descrevem totalmente os fenômenos sociais. Em particular, os valores absolutos dos gastos não foram considerados nem no caso da saúde nem no da educação. Mas certamente os gráficos servem para nos desenganar de crenças simplistas. Os fatos têm um viés liberal bem conhecido – ou neoliberal, conforme o caso.
Quais são então as técnicas matemáticas que permitem aos computadores realizarem procedimentos de classificação e modelagem em casos mais complexos? Para falar sobre isso, num próximo artigo vamos voltar aos clássicos da matemática europeia dos séculos XVIII e XIX.