por Étienne Ghys
Faz pouco menos de cem anos, os matemáticos chegaram lá: entre o verdadeiro e o falso, entre o possível e o impossível, há nuances. Eles levaram um bom tempo para isso! Todo mundo sabe muito bem que na vida de cada dia não é sempre fácil distinguir o verdadeiro do falso, e que, algumas vezes, é simplesmente impossível.
E, no entanto, os matemáticos são ainda muitas vezes apresentados como pertencendo a um mundo caricatural e frio, onde se está ou certo ou errado.
O século dezenove, com seu otimismo e suas certezas, deu lugar a um século vinte cheio de dúvidas e de complexidades. E esta evolução não se encontra, é claro, somente no domínio da matemática. Basta evocar o “princípio da incerteza” da mecânica quântica, ou a relatividade de Einstein, para constatar que também os físicos colocaram em questão algumas de suas certezas, aproximadamente na mesma época. Além disso, poderíamos encontrar várias situações análogas no exterior do domínio das ciências.
A quadratura do círculo
A quadratura do círculo é um problema impossível. Na verdade, se trata de um problema da geometria do plano, que remonta à Antiguidade.

É dado um círculo, e dispõe-se de uma régua e de um compasso. O desafio consiste em construir um quadrado cuja área seja igual àquela do círculo. Por que esta questão é interessante? Para dizer a verdade, hoje em dia não é mais muito interessante. Mas pode-se considerar que houve um tempo no qual um topógrafo podia querer encontrar a superfície de um tanque circular. Nós sabemos que esta superfície é ?R² (pi-R-ao quadrado), onde R designa o raio do círculo e ? (“pi”) é a célebre constante que vale aproximadamente 3,14… Dito de outra maneira, a quadratura do círculo consiste em determinar o valor de ? com uma régua e um compasso. Mas por que isso, se a minha calculadora me diz que ?=3,14159265358979… , e isso satisfará todos os topógrafos do mundo por muito tempo ainda? Isso não impede que este enigma tenha perseguido os geômetras por muitos séculos, até que, em 1882, o matemático Lindemann demonstrou que é impossível!
É de certa maneira como se o número ? não existisse, pois não podemos construí-lo. Mas é claro que, para construí-lo, são necessários instrumentos, e neste caso se trata de uma régua e de um compasso. Se sou autorizado a utilizar outros instrumentos, como por exemplo um computador, eu posso escrever um pequeno programa que vai mostrar na minha tela as casas decimais de ? uma a uma. Talvez o computador demore muito tempo para encontrar a milésima casa decimal, mas ele terminará por calculá-la. O número ? não pode ser construído com uma régua e um compasso, mas ele é (em princípio) calculável por um computador (com uma precisão arbitrária).
A incompletude
No início do século vinte, os lógicos deram uma boa lição de modéstia aos matemáticos, mas também aos cientistas e aos filósofos. Assim como alguns números existem mas não podem ser construídos, de certos enunciados não se pode demonstrar nem que eles são verdadeiros nem que eles são falsos. Trata-se do teorema de Gödel, que data de 1931. Não é questão aqui de enunciá-lo com precisão: para isso, seria necessária uma longa exposição.

De certa maneira, os juristas conhecem este teorema há muito tempo. Simplifiquemos ao extremo o problema que se apresenta à justiça. Trata-se de determinar se um acusado é inocente ou culpado de um crime. Para isso, o tribunal penal possui um certo número de instrumentos, colocados à sua disposição pelo código penal, por exemplo. Ela dispõe também de um certo número de fatos, testemunhos, etc., estabelecidos durante a investigação. E assim a máquina judicial funciona. Algumas vezes ela pode estabelecer a inocência, outras ela pode estabelecer a culpabilidade. Mas algumas vezes, ela reconhece que não pode estabelecer nem uma coisa nem outra; os instrumentos dos quais dispõe são insuficientes para concluir, e há absolvição. Há muito tempo que os juristas compreenderam que eles não podem sempre acessar a verdade!
Quando raciocinamos, temos à nossa disposição um certo número de enunciados “sólidos” sobre os quais podemos nos apoiar: chamamo-los de axiomas. E dispomos também de algumas regras de raciocínio: o código penal do matemático. Trata-se de estabelecer se um enunciado é verdadeiro ou falso. Algumas vezes chegamos a mostrar que ele é falso. Outras vezes, que ele é verdadeiro. E algumas vezes é impossível de chegar a uma coisa ou a outra. Insistamos: não é que eu não tenha conseguido fazê-lo, é que podemos demonstrar que existem enunciados cuja verdade ou falsidade não pode ser demonstrada. Dizemos que eles são “indecidíveis”.
Nosso método matemático é incompleto quanto ao seu poder.
Poderíamos tentar dizer que basta aumentar o número de axiomas, ou acrescentar algumas regras de raciocínio, para adicionar força à matemática – mas o teorema de Gödel é implacável. Quaisquer que sejam os axiomas que acrescentemos, estaremos diante de uma alternativa bem desagradável. Ou teremos adicionado axiomas demais e nossa máquina de raciocinar será tão ruim que ela se tornará contraditória, permitindo demonstrar qualquer coisa e também o contrário disto; ou sobrarão enunciados indecidíveis. Nós devemos portanto aceitar o fato de que certas verdades nos são inacessíveis. Bela lição.
Verdadeiro ou falso?

Podemos então nos perguntar que significam as palavras “verdadeiro” e “falso”. Poderíamos pensar, ingenuamente, que um enunciado é verdadeiro se podemos demonstrá-lo, e falso se podemos demonstrar sua negação. Mas então, o teorema de Gödel nos conduziria à conclusão de que certos enunciados não são nem verdadeiros nem falsos. Isso não nos parece aceitável. É necessário que todos os enunciados sejam verdadeiros ou falsos!
Voltemos à nossa analogia jurídica. Quando um tribunal penal pronuncia uma absolvição porque ele não pode provar a culpabilidade de um acusado, ela não se pronuncia sobre esta culpabilidade; no entanto, o acusado ou é culpado ou não o é.
É mais ou menos a mesma coisa na matemática. Consideramos frequentemente que os raciocínios matemáticos e os axiomas são um modo de explorar um “mundo matemático abstrato” (o chamamos de modelo) no qual todos os enunciados são verdadeiros ou falsos. O teorema de Gödel toma então uma forma mais impressionante: certos enunciados são verdadeiros (em um modelo), e no entanto não podem ser demonstrados.
O fato de um enunciado ser demonstrável depende do sistema de axiomas utilizados, enquanto a sua veracidade depende do modelo matemático escolhido, aquele que nos propomos estudar.
Em seguida, vem a questão da escolha do modelo utilizado pelos matemáticos. Trata-se agora de uma discussão de natureza filosófica. A maior parte dos matemáticos pensam que seu trabalho consiste em explorar um mundo matemático que tem uma verdadeira “existência”, quase concreta, e que é comum a todos os seres humanos (ou mesmo extraterrestres?). Dito de outra maneira: vários matemáticos pensam que existe um modelo privilegiado, o qual eles “visitam”, e que cada enunciado matemático é portanto verdadeiro ou falso.
Tente então perguntar a matemáticos o que a palavra “verdadeiro” significa para eles: você verá que as respostas são raramente claras. Na verdade, apenas alguns poucos se colocaram esta questão, que está entretanto no coração de sua atividade.
Um “exemplo”
Durante muito tempo, os matemáticos pensavam que o teorema de Gödel era apenas uma elucubração de lógicos e que os enunciados da vida (matemática!) de todos os dias são decidíveis na prática. Entretanto, existem exemplos relativamente concretos de enunciados indecidíveis. Infelizmente, eles são um pouco complicados para que possamos explicá-los aqui.
Mas eis um enunciado “que poderia muito bem ser verdadeiro e indecidível”. Dizemos que dois números primos[1] são gêmeos se a diferença entre eles é 2, como por exemplo 3 e 5, ou 5 e 7, ou ainda 881 e 883. Há muito tempo se pergunta se existe uma infinitude de números primos gêmeos.
O enunciado “há uma infinitude de números primos gêmeos” descreve uma propriedade dos números inteiros naturais. Dizer que ele é verdadeiro ou falso depende da escolha de um modelo para os inteiros naturais, mas ainda assim a maior parte dos matemáticos pensa que o conjunto dos números naturais “existe”, quer dizer que eles são privilegiados de um modelo em particular. O enunciado é portanto verdadeiro ou falso, mesmo se sou incapaz de dizer mais sobre isso.
É possível que um dia um matemático encontrará uma demonstração de que este enunciado é verdadeiro, ou uma demonstração de que ele é falso; mas é também possível que este enunciado seja indecidível e falso, ou ainda indecidível e verdadeiro.
Calculável
Suponhamos que você queira fazer o piso de sua cozinha com azulejos do seguinte tipo:
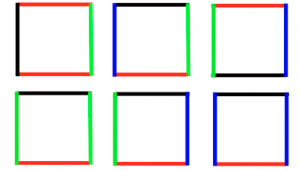
São simplesmente quadrados cujos lados são coloridos. Você assume então uma regra: você colocará um azulejo ao lado de outro unicamente quando os lados adjacentes tiverem a mesma cor (não vale girar ou inverter os azulejos: apenas deslocá-los). Como falamos aqui de matemática, nós não hesitaremos em supor que a sua cozinha é infinita 🙂 mas eu suponho mesmo assim que há apenas um número finito de cores (digamos, azul, vermelho, verde e preto, por exemplo), e que os tipos de azulejo que eu me proponho a utilizar são dados de partida (6 tipos, no exemplo acima).
Como determinar se é possível? Gostaríamos de programar um computador para que ele responda à questão. Forneceríamos ao programa como dados de entrada o número de tipos de azulejos dos quais dispomos, as cores dos lados, e pressionaríamos a tecla Enter. O programa calcularia e responderia: “sim, é possível, seus azulejos coloridos podem mesmo cobrir o piso da sua cozinha infinita”, ou “não, é impossível”.
Pois bem, um tal programa não existe. É um teorema de Robert Berger, datando de 1966 e fundado sobre um resultado fundamental de Turing de 1936.

Dito de outra maneira: certos problemas não podem ser resolvidos por um computador, não importa quão potente ele seja. É uma outra forma de indecidibilidade.
Complicado
A chegada dos computadores nos fez perder consciência de um outro fato cujo alcance científico e filosófico é considerável. Certos fatos são verdadeiros e demonstráveis mas suas demonstrações são tão longas que tudo se passa como se elas não existissem. Voltemos ao exemplo do computador ao qual peço para calcular as casas decimais do número ?. Suponhamos que eu busque a bilionésima casa, por exemplo. Se eu fiz algo errado, se meu programa é ingênuo, é claro que meu computador começará um cálculo desmesuradamente longo, e o tempo necessário para isso será provavelmente bem superior à idade do universo! Para que então um tal cálculo? Qual é o sentido da frase “eu posso calcular a bilionésima casa decimal de ?” se para isso é necessário esperar um período tão longo que eu não posso aceitá-lo? Talvez eu tenha feito algo errado? Talvez ao dar instruções diferentes para o mesmo computador, ele poderia encontrar a bilionésima casa decimal em 15 minutos? Mas também aqui os lógicos nos levaram à modéstia. Existem enunciados bem pouco complicados, que são demonstráveis mas que não podem ser demonstrados em um tempo razoável. Os comprimentos das provas são incomensuravelmente maiores que os comprimentos dos enunciados que devem ser demonstrados. É possível demonstrá-los, mas é impossível fazê-lo em um tempo útil. Eles estão portanto fora do alcance do nosso entendimento.
Provável
O DNA de um suspeito, encontrado no local do crime, é uma prova de culpabilidade? Falando estritamente, não é impossível que duas pessoas diferentes tenham exatamente o mesmo DNA, mas é muito, muito, muito improvável (esqueçamos o caso dos gêmeos).
Se duas pessoas lançam mil vezes consecutivamente uma moeda, qual é a probabilidade que elas encontrem exatamente a mesma sequência de caras e de coroas? Uma chance em 10 715 086 071 862 673 209 484 250 490 600 018 105 614 048 117 055 336 074 437 503 883 703 510511 249 361 224 931 983 788 156 958 581 275 946 729 175 531 468 251 871 452 856 923 140 435 984577 574 698 574 803 934 567 774 824 230 985 421 074 605 062 371 141 877 954 182 153 046 474 983581 941 267 398 767 559 165 543 946 077 062 914 571 196 477 686 542 167 660 429 831 652 624 386837 205 668 069 376. O que equivale a dizer que é “impossível”.
A teoria das probabilidades fez um esforço formidável durante o século 20. Também aí, trata-se de pensar o possível e o impossível, e este novo instrumento tem um poder incrível.
Concluamos que, de fato, a matemática hoje não é mais aquela do verdadeiro e do falso: entre o verdadeiro, o demonstrável, o provável, o calculável, o coerente, o efetivo, o decidível etc., ela propõe abordagens bem mais sutis.
Étienne Ghys é matemático, diretor de pesquisa do CNRS na Escola Normal Superior de Lyon. É membro da Academia Francesa de Ciências, membro correspondente da Academia Brasileira de Ciências (ABC) e pesquisador honorário do Instituto de Matemática Pura e Aplicada (Impa), no Rio de Janeiro. Participa do Conselho Científico do recém-nascido Instituto Serrapilheira. Este artigo foi originalmente publicado no site Image des Mathématiques, do CNRS (Conselho Nacional de Pesquisa Científica da França). Tradução de João Cortese.
[1] Lembremos que um número inteiro maior ou igual a 2 é dito primo se ele não pode ser escrito como o produto de dois números inteiros menos que ele. Por exemplo, 5 é primo, mas 6 não, pois este é igual a 2 vezes 3. Você conseguiria determinar se 8999737 é primo? Quanto tempo você levaria para sabê-lo? Quanto tempo levaria o seu computador?
Para saber mais:
– Doxiads, A. K., Papadimitriou, C. H., Papadatos, A., Di Donna, A., & Santos, A. B. Logicomix: uma jornada épica em busca da verdade. WMF Martins Fontes, 2000.
– Douglas R. Hofstadter. Godel, Escher, Bach: um entrelaçamento de gênios brilhantes. Editora UNB, 2001
No Estado da Arte
A verdade é a mesma em Cambridge e em Madras? – Dois olhares sobre a matemática